
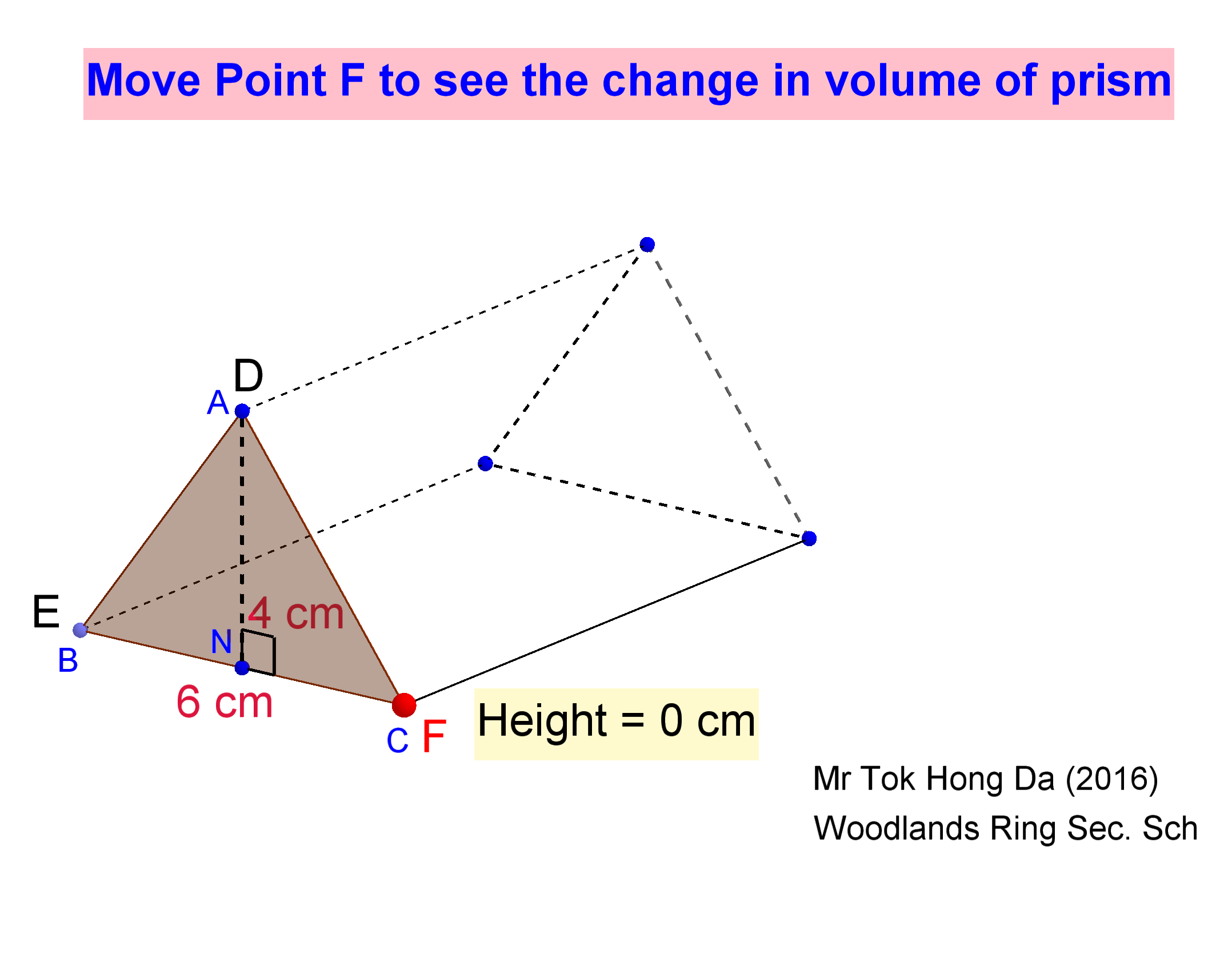
Although much progress has been made in advancing research into tensegrity systems and their application in science and engineering, there are currently no universally accepted design guidelines for their dialectic form finding, tuning their behavior, and guiding their transformation into active systems. Therefore, they are good candidates for smart applications. They are materially and mechanically efficient form-found structures that can also integrate sensors and actuators. Their self-equilibrated prestressed state is a result of their topology and geometry which define their statical (self-stress) and kinematical (mechanisms) properties. Tensegrity structures are reticulated frameworks composed of axially loaded elements in a stable self-equilibrated prestressed state. The examples attest how the proposed approach, which combines topological as well as geometrical considerations, can be used to decipher the state of complex systems.
#TRIANGULAR PRISM NET SERIES#
A series of examples that highlight the flexibility of network equilibrium models are included in the paper. Consequently, the equilibrium state of complex self-equilibrated systems can be obtained through the study of individual cell equilibria and their interactions. A new approach for the analysis of self-equilibrated networks is proposed they are modeled as a collection of cells, predefined elementary network units that have been mathematically shown to compose any self-equilibrated network. In this paper, network equilibrium models are revisited through graph-theory laws and attributes with special focus on systems that can sustain equilibrium in the absence of external perturbations (self-equilibrium).
They have been widely employed in both science and engineering to study the behavior of complex systems under various conditions, including external perturbations and damage.

Network equilibrium models represent a versatile tool for the analysis of interconnected objects and their relationships. Although the study focuses on selected configurations and arrangements, the generalization of the ideas and findings included in this paper can lead to the generation of tensegrity structures with predefined static as well as kinematic properties, thus further enabling the application of tensegrity systems in science and engineering. Analytical solutions of the degeneracy space for configurations resulting through adhesion and the fusion of two cells with the removal of two edges are described using symbolic calculations on the rigidity matrices of tensegrity structures. In addition, an interpretation of the degeneracy of tensegrity structures in the case of self-stressable mechanisms is also presented. Parametric descriptions of the infinitesimal displacements in the case of trivial and finite mechanisms are derived through the analysis of rigid assemblies corresponding to the rigid parts of the structure.

The creation of finite and infinitesimal mechanisms in tensegrity structures is described through the adhesion of cells sharing less than nodes (being the dimension of the workspace), and through the fusion of cells with the removal of two edges. This article discusses the mechanism creation through the integration of mobility conditions in the generation of tensegrity structures using cellular morphogenesis. Cellular morphogenesis represents a generative process for the composition of complex tensegrity structures based on elementary cells. Tensegrity structures are self-equilibrated statically and kinematically indeterminate structures.


 0 kommentar(er)
0 kommentar(er)
